(本文使用https://www.codecogs.com/进行latex渲染,若latex公式有问题,请开启全局梯子)
一直以来SVM都停留在一看就大概知道,一上手推导就傻眼的阶段。实际上还是没有真正地理解了SVM的精髓,对于 关键定理 这里总是囫囵吞枣。看一看网上大部分的教程,也都是以推导为主,所以想手写实现一下,加深理解。
talk is cheap, show me the code.
假设我们已经艰难地推导到了最后,得到了SVM的对偶问题上:
这时候,我们需要求解一系列的值了,只要得到了
的值,那么W,b 就好求了。 西瓜书 上也就到了这里,告诉我们这是一个二次规划问题(这我也不会啊😭)。顺理成章地引入了 SMO 算法来求解
,得到了
后,对W,b进行更新迭代:

即可求出超分类面,也就是分类函数:
=W^Tx+b&space;=&space;\sum_{i=1}^m\alpha_{i}y_{i}x_{i}^T+b)
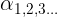 ,实际上这里我也不能明白SMO的精髓,只能按着 [wikipedia SMO序列最小优化算法](https://zh.wikipedia.org/wiki/序列最小优化算法) 中介绍的的流程来进行计算了😏。

其中,$L$和$H$分别是$\alpha_{2}^{new}$ 的下界和上界。特别地,有:

推导过程实在繁琐,我们这里直接拿作者的解析解:
> 记
,实际上这里我也不能明白SMO的精髓,只能按着 [wikipedia SMO序列最小优化算法](https://zh.wikipedia.org/wiki/序列最小优化算法) 中介绍的的流程来进行计算了😏。

其中,$L$和$H$分别是$\alpha_{2}^{new}$ 的下界和上界。特别地,有:

推导过程实在繁琐,我们这里直接拿作者的解析解:
> 记 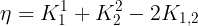 , 这里
, 这里) 为核函数,用于将低维空间的数据映射到高维空间,我们以后再谈;
> 记
为核函数,用于将低维空间的数据映射到高维空间,我们以后再谈;
> 记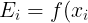-y_{i}) ,也就是更新后的SVM预测值与真实值的误差。
得到:
,也就是更新后的SVM预测值与真实值的误差。
得到:
&space;}{\eta})
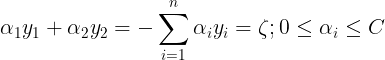
,\\&space;H=min(C,&space;C+\alpha_{2}^{old}-\alpha_{1}^{old})&space;\end{aligned}&space;\right.)
,\\&space;H=min(C,&space;C+\alpha_{2}^{old}+\alpha_{1}^{old})&space;\end{aligned}&space;\right.)
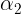 更新公式为:
更新公式为:
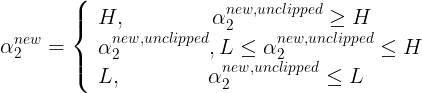
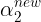 后,
后,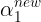 也可以同样求出来:
也可以同样求出来:
)
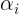 进行选取,便可以进行优化更新了。
根据Platt的原文提供的伪代码,我们有如下实现**(PC或MAC下加载以下代码展示)**:
## 数据分布如下:
绘制:


## 致谢
本文参考文章:
[理解支持向量机的三重境界](https://www.cnblogs.com/v-July-v/archive/2012/06/01/2539022.html)
[看了这篇文章你还不懂SVM你就来打我](https://zhuanlan.zhihu.com/p/49331510)
[一起学SVM之python实现SMO算法](https://www.bilibili.com/video/BV145411s7nY?t=3224)
进行选取,便可以进行优化更新了。
根据Platt的原文提供的伪代码,我们有如下实现**(PC或MAC下加载以下代码展示)**:
## 数据分布如下:
绘制:


## 致谢
本文参考文章:
[理解支持向量机的三重境界](https://www.cnblogs.com/v-July-v/archive/2012/06/01/2539022.html)
[看了这篇文章你还不懂SVM你就来打我](https://zhuanlan.zhihu.com/p/49331510)
[一起学SVM之python实现SMO算法](https://www.bilibili.com/video/BV145411s7nY?t=3224)
