这篇文章是im2latex系列的第一篇,希望能够讲清楚基于attention的Sequence-to-Sequence和Beam Search的一些基本概念。
直接看代码如果你对Seq2Seq和熟悉了,想直接跳到tensorflow代码部分的话。
介绍
在上一篇命名实体识别中,我介绍了一个相对简单的任务:如何去预测一个单词的属性。如果是翻译之类的任务就需要设计比较复杂的系统了。我们知道最近神经机器翻译已经取得了很大的突破—(几乎)可以达到人类的水平了(像Google翻译已经被大量应用在生活中,具体参与文章)。这些新的结构依赖于一种称为Encoder-decoder的的结构,可以用于产生特定实体的目标序列。
阅读这篇文章前,假定你对深度学习的基础知识(卷积CNN,长短时记忆LSTM…)之类的基本概念已经很熟悉了。如果你还对这些CV和NLP方面的知识不是很熟悉,建议先看看大名鼎鼎的斯坦福公开课CS231n和CS224n。
Sequence to Sequence 基本概念
先介绍我们使用的模型中最重要的Sequence to Sequence框架。先从翻译任务中最简单的版本说起。
举个🌰,翻译”how are you“成中文“干哈呢”.(法语:comment vas tu)
普通Seq2Seq
Seq2Seq模型依赖于encoder-decoder结构。Encoder端对输入序列编码,然后Decoder端产生解码后的目标序列。
编码器
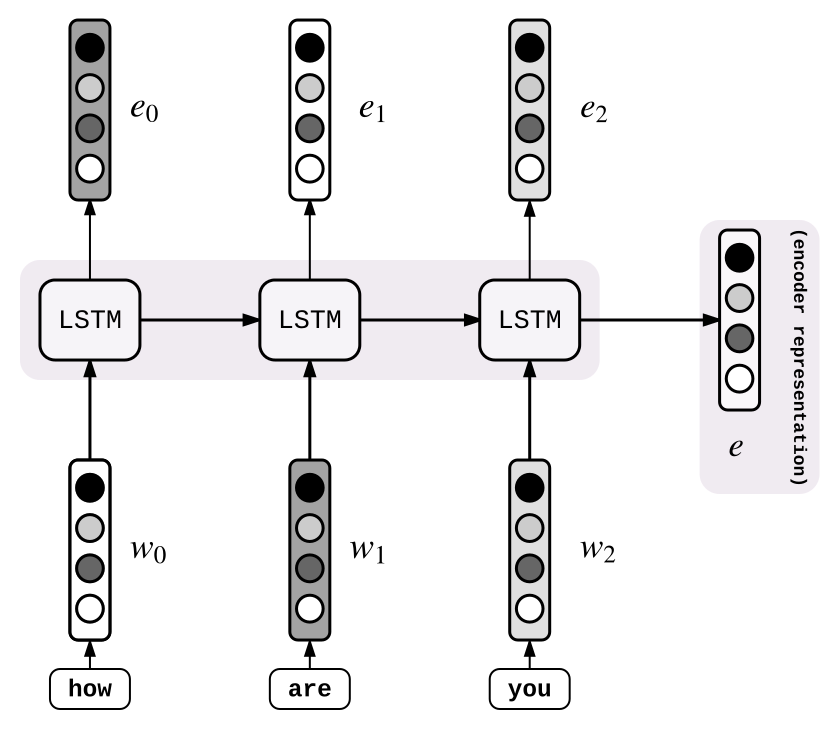
上个例子中我们的输入序列是“how are U”。每个输入序列的单词被转化为了一个向量$w\in R^{d}$(这一过程通过速查表实现)。上个例子中有3个单词,这样输入将会被转化为$[W_{0}, W_{1}, W_{2}\in R^{d\times3}]$.之后,输入向量序列进入LSTM,存储下LSTM输出的最后一层隐藏层状态:这就是编码器的编码结果e了。写下这里的隐藏层状态: [$e_{0}, e_{1}, e_{2}$] (这里的$e=e_{2}$)。
解码器
现在有了向量 $e$ 捕获了输入序列的信息,下面使用它来一个单词一个单词的产生目标单词序列。隐层状态 $e$ 和特殊的开始标记 $W_{sos}$ 向量作为输入来送入LSTM单元。LSTM计算了下一个隐藏层状态$h_{0}\in R^{h}$。然后应用函数$ g : R^{h}\Rightarrow R^{V}$ ,这样$s_{0} := g(h_{0})$ 是词汇表中同样大小的向量。
\[h_{0} = LSTM(e, w_{sos})\],
\[s_{0} = g(h{_0})\],
\[p_{0} = softmax(s_{0})\],
\[i_{0} = argmax(p_{0})\]之后,$s_{0}$经过softmax来正则化后进入概率矩阵$p_{0}\in R^{V}$ 。每个实体的 $p_{0}$ 用来衡量它和单词表中的单词的相似度。可以说“干”具有最高的概率(也就说$i_{0} = argmax(p_{0})$ 对应“干”的索引)。得到对应的向量$W_{i_{0}} = W_{干}$,然后重复这个过程:继续将隐藏层状态$h_{0}$ 和 $W_{干}$输入LSTM,LSTM再输出对应第二个词的概率矩阵$p_{1}$…为:
\[h_{1} = LSTM(h_{0}, w_{i_{0}})\],
\[s_{1} = g(h{_1})\],
\[p_{1} = softmax(s_{1})\],
\[i_{1} = argmax(p_{1})\],
当解码器遇到特殊停止符(往往是”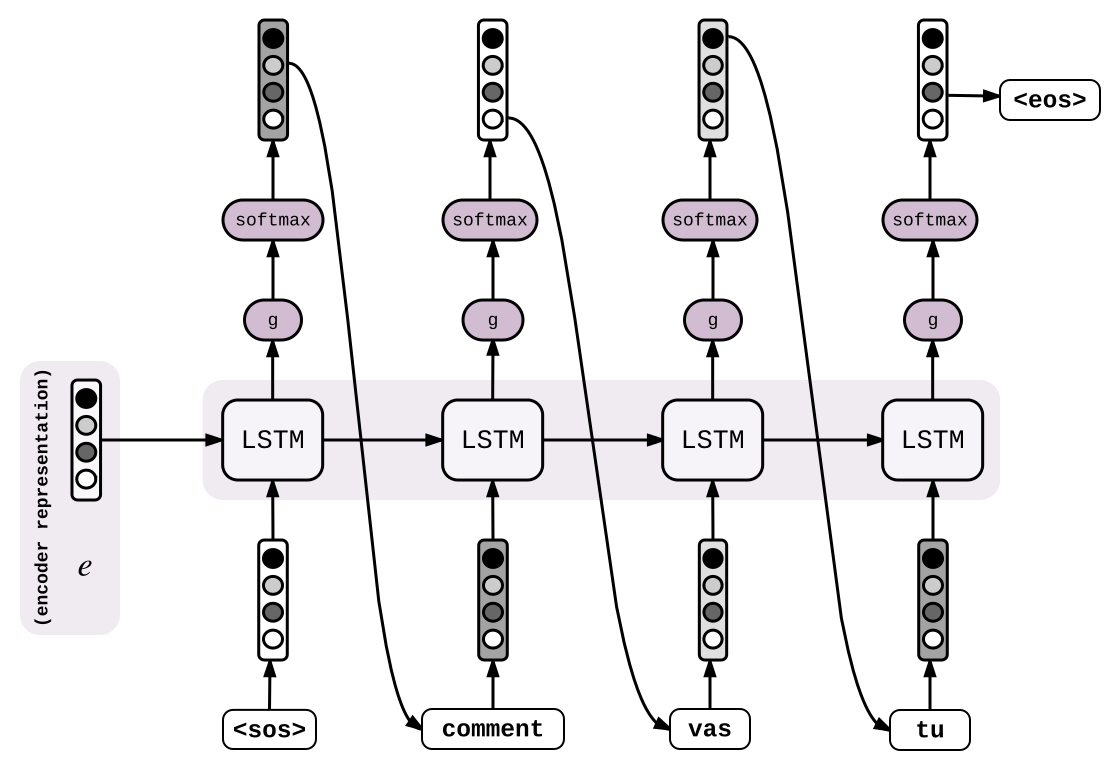
直觉上,隐藏层向量还未被解码的信息。
上述方法旨在下一个单词在句子开头已知情况下的条件概率分布: \(P[y_{t+1}|y_{1},...,y_{t},x_{0},...,x_{n}]\) 简写为: \(P[y_{t+1}|y_{t},h_{t},e]\)
加入attention的Seq2Seq
托attention的福,这两年上面的Seq2Seq模型已经大变样了。Attention是一种让模型在解码时学习集中关注输入序列特定部分的模型,而不仅依靠解码中LSTM隐藏层的部分。关于attention的详细介绍请参阅文章。这里我们稍微修改一下上面的公式,在LSTM的输入部分加入一个新的向量$C_{t}$ : \(h_{t} = LSTM(h_{t-1}, [w_{i_{t-1}}, c_{t}])\)
,
\[s_{t} = g(h_{t})\],
\[p_{t} = softmax(s_{t})\],
\[i_{t} = argmax(p_{t})\],
向量 $c_{t}$ 就是注意力(或称上下文)向量。每一步解码的过程计算一个新的注意力向量。首先,使用函数$f(h_{t-1}, e_{e_{t^{old}}})\Rightarrow \alpha_{t_{old}} \in R$ 计算编码器每一个隐藏层状态$e_{t_{old}}$ 的分数;之后使用softmax正则化$\alpha_{t_{old}}$,然后与$e_{t_{old}}$ 加权计算$c_{t}$: \(\alpha_{t_{old}} = f(h_{t-1}, e_{t_{old}})\)
,
\[\overline{\alpha} = softmax(\alpha)\],
\[c_{t} = \sum_{t_{old}=0}^n\overline{\alpha}_{t_{old}}{e_{t_{old}}}\],
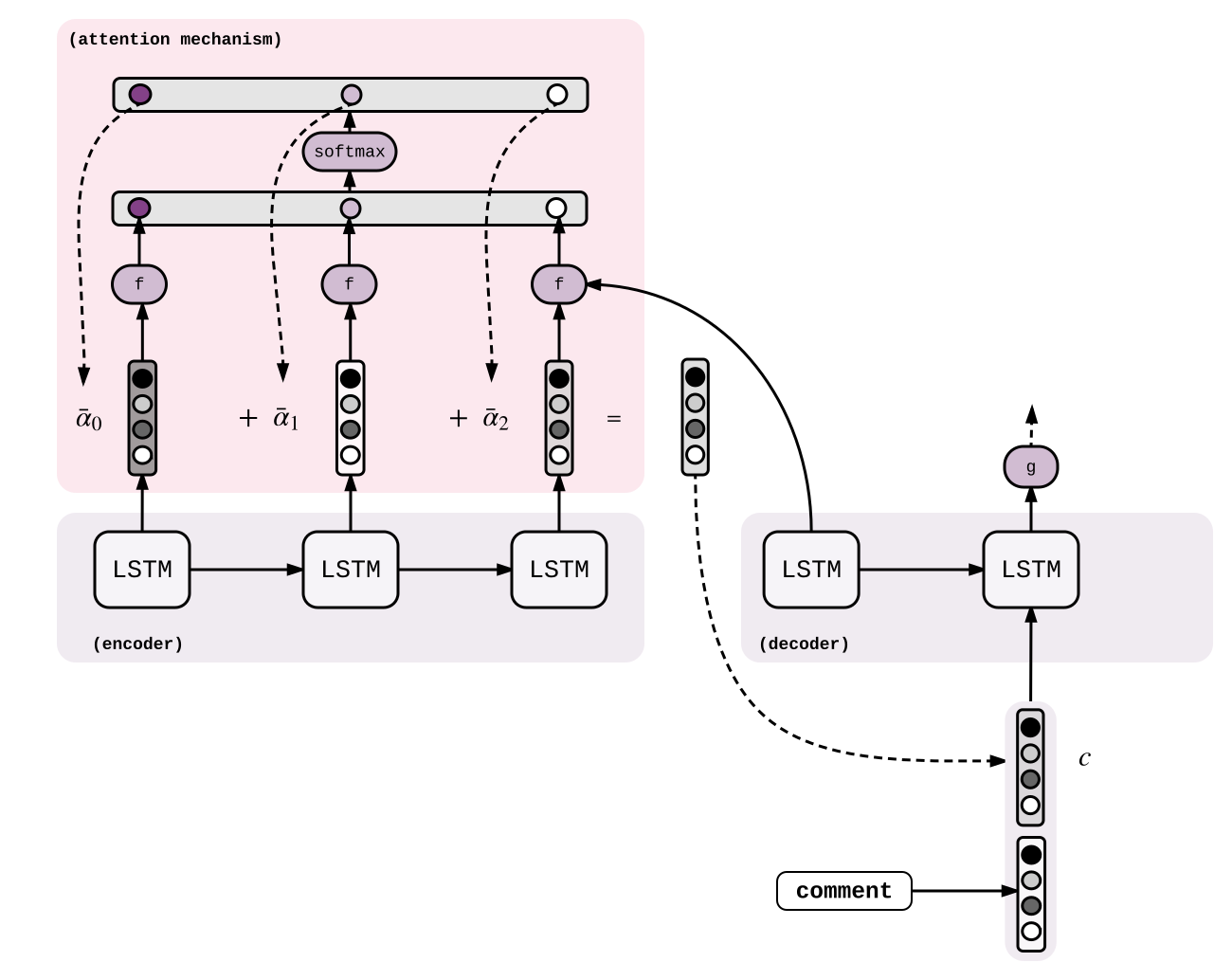
在这里,计算注意力向量$\alpha_{t_{old}}$ 的函数$f$那可就多啦,一般也就下面几种:
\[f(h_{t-1},e_{t_{old}})=\begin{cases}h^{T}_{t-1}e_{t_{old}}&\text{dot}\\h^{T}_{t-1}We_{t_{old}}&\text{general}\\v^{T}tanh(W[h_{t-1},e_{t_{old}}])&\text{concat}\end{cases}\],
这样子注意力权重$\overline{\alpha}$ 很容易解释了。当产生单词vas的时候(对应英语are),我们期望$\overline{\alpha_{are}}$ 接近1,而$\overline{\alpha_{how}}$和$\overline{\alpha_{you}}$接近0。直觉上注意力向量$c$大致接近are的隐含层向量,它有助于产生法语单词vas。
通过将注意力权重送入矩阵(行=输入序列,列=输出序列),我们就可以“对齐”输入的英语单词和输出的法语单词了(参见文章第六页)。关于Seq2Seq模型还有好多可以探讨的地方,比如编码器可以双向处理输入序列,限于篇幅,这里不再展开了。
训练
如果第一次产生的序列并不太确定是comment还是vas(训练开始很大程度都可能遇到)的话,会怎么样呢?那整个输出序列就全乱了,模型也很难学到什么东西了….
如果我们使用训练中预测的输出来作为下一步的输入,错误就会一直累积下去,模型很难收敛到正确的输入分布上。这会使训练过程很慢甚至不可训练。为加快训练过程,可以将真实的输出序列 (<sos>comment vas tu)送入解码LSTM来预测每次下一步骤产生的输出 (commentvas tu <eos>)。
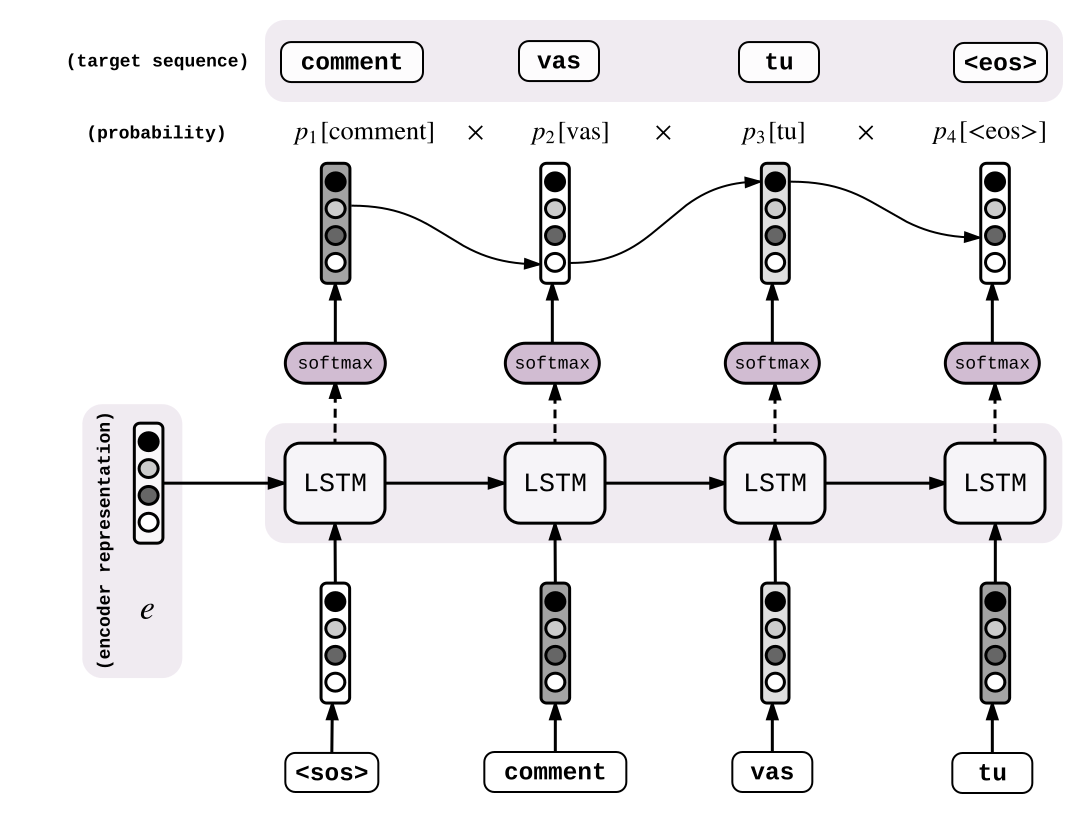
解码器在每一步输出概率矩阵$p_{i}\in R^{V}$。对于每一个给定的目标输出序列$y_{1},…y_{n}$,我们在每一步计算每个输出的概率: \(P(y_{1},...y_{m}) = \prod\limits_{i=1}^m p_{i}[y_{i}]\) 这里$p_{i}[y_{i}]$代表在第i个解码步骤中提取第$y_{i}$个实体的概率$p_{i}$。这样,我们可以计算真是的目标序列概率。一个完美的系统可以输出目标序列接近1的概率,所以我们训练网络来最大化输出目标序列的概率,也就是最小化这个目标: \(-\log P(y_{1},...,y_{m}) = -\log \prod\limits_{i=1}^m p_{i}[y_{i}]\\ = -\sum_{i=1}^{n}\log p_{i}[y_{i}]\)
,
在我们这个例子中,也就等于 \(-\log p_{1}[comment]-\log p_{2}[vas]-\log p_{3}[tu]-\log p_{4}[<eos>]\) 。这不就是标准的交叉熵吗!我们实际上在最小化目标分布和我们模型(概率$p_{i}$)预测的输出分布之间的交叉熵!
解码
上述讨论中主要的问题是对于同一个模型,我们可以有不同的行为。特别在加速训练的时候。
那在推理/测试阶段呢?是不是有另外的方式来解码(翻译)一个句子呢?
的确,在测试阶段有两种方法来解码(测试就是翻译一个我们还没有翻译过的句子)。一种就是我们文章开始提到的解码方式:greedy decoding。它包含了上次预测的值最可能进入下次的方式,也是最自然的解码方式。

但你不觉得这种方式在累积误差吗?
即便训练好了模型,也可能恰巧模型出了点小毛病(可能首次预测 vas 的概率高于 comment )。那整个的解码过程就彻底崩了!
有种更好的解码过程,叫Beam Search:相对于仅预测最高分数的输出,可以在预测的时候跟踪最有可能的K个候选(比如K=5,我们就使用5作为Beam Search的大小)。在每一个新的预测(解码)步骤,对每5个候选我们可以有V个新的输出。这一下子就有了5V个心得候选。然后再选择其中5个最靠谱的,这一过程继续下去…. 上公式,定义$H_{t}$为第t个步骤的解码候选集合。 \(H_{t} := {(W^{1}_{1},...W^{1}_{t}),...(W^{k}_{1},...W^{k}_{t})}\) 再举个🌰,如果k=2,这时可能的集合就是 \(H_{2} := {(comment vas), (comment tu)}\) 现在我们考虑所有可能的候选$C_{t+1}$,从$H_{t}$中产生新的输出: \(C_{t+1} := \bigcup^{k}_{i=1}\{(w^{i}_{1},...w^{i}_{i},1),...(w^{i}_{1},...w^{i}_{i},V) \}\) 保持K个最高的得分序列。在我们的例子中: \(C_{3} = \{(comment,vas,comment), (comment,vas,vas), (comment,vas,tu)\}\bigcup \{(comment,tu,comment)\}\)
我们假设最高的两个是:
\(H_{3} := \{ (comment, vas, tu),(comment, tu, vas) \}\)
每次候选遇到 <eos> 标志,就返回最高得分的候选。
如果我们使用Beam Search,因为我们保持着最优候选集合,初始步骤的小错误会在下一步被修正。
结论
本文介绍了Seq2Seq的几个概念。可以看到训练和解码部分不太一样。也介绍了两种解码方法:greedy和beam search。虽然beam search可以取得较好的结果,但是它依然存在exposure bias。训练阶段,模型也不会exposed到错误。他也会有Loss-Evaluation mismatch。模型是通过输出token级别的交叉熵来优化的,而我们更感兴趣的是整个句子结构的重建….
下面,让我们应用Seq2Seq到图像生成LaTex上吧!
[看代码](https://anxingle.github.io)
Seq2Seq经典论文:
- Sequence to Sequence Learning with Neural Networks
- Neural Machine Translation by Jointly Learning to Align and Translate
- Effective Approaches to Attention-based Neural Machine Translation
- Neural Machine Translation in Linear Time
- Convolutional Sequence to Sequence Learning
- Attention Is All You Need
试图解决一些一些局限性的文章:
article translated from Guillaume Genthial Blog
